LeetCode #17 - Letter Combinations Of A Phone Number
November 14, 2020
Hello fellow devs 👋! Today we are going to discuss a popular problem which is asked by many tech giants in coding interviews.
Problem Statement
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
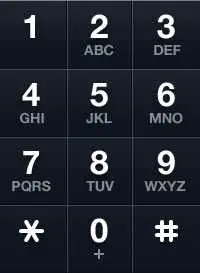
Constraints:
- 0 ≤ digits.length ≤ 4
digits[i]is a digit in the range['2', '9'].
Examples
Example 1:
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]Example 2:
Input: digits = ""
Output: []Example 3:
Input: digits = "2"
Output: ["a","b","c"]Analysis
We all have seen above image in the good olden days 💗 where we used to have better music and better life 😃. Before the time of touch screen, mobile phones used to have this keypad where each button represented some symbols — numbers, letters, etc.
In this question also, we need to find all the combinations of letters which can be obtained if a number is pressed. For e.g., from the above image 3 represents def and 5 represents jkl so if someone were to press 35, they will get one of the following combinations —
dj, dk, dl, ej, ek, el, fj, fk, flWe need to find these combinations. If we look at it more closely, there are a few things to notice —
- We need to take care of only numbers
2,3,4,5,6,7,8,9. - There can be a maximum of 4 characters in a given string.
- The result needs to be the Cartesian product of the given letters’ combination.
Approach
How do we solve it? If you are thinking about recursion, then you are on the right track. At each stage of recursion there will be a digit that will represent some characters, and then we will recursively send the next digit to look for those set of characters that could be appended in our result string.
We can follow below steps —
- Construct an array where each index represents the corresponding letters on the keypad corresponding to that number. Since there are no letters with respect to
0and1, for the sake of ease of accessibility, we will put dummy values on those indices. Such an array will look something like this —
lettersAndNumbersMappings = [
"Anirudh",
"is awesome",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
]- Write a helper function which will contain the crux of our logic. This function will be called recursively.
- In the recursive function, we should have a terminating condition. In our case, think when our recursion will stop 🤔? It will stop when we have scanned all the characters in the given string. At that point, we will return.
- If the terminating condition is not met then we will first find the letters corresponding to the current characters in the given string by referring to our mappings array.
- We will then loop for all the characters in the string obtained in the previous step and call make recursive calls with the strings after appending the current character and the string in the previous step.
Time Complexity
The numbers in input string can represent strings of length of 3 or 4. Let m be the number of digits that map to 3 letters and n be the number of digits that map to 4 letters. Thus, the overall time complexity will be O(3m × 4n).
Space Complexity
The recursive call will use the stack memory equal to O(3m × 4n) and this will be the space complexity.
Code
Java
public class LetterCombinationsOfAPhoneNumber {
private static List<String> letterCombinations(String digits) {
// Resultant list
List<String> combinations = new ArrayList<>();
// Base condition
if (digits == null || digits.isEmpty()) {
return combinations;
}
// Mappings of letters and numbers
String[] lettersAndNumbersMappings = new String[]{
"Anirudh",
"is awesome",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
};
findCombinations(combinations, digits, new StringBuilder(), 0, lettersAndNumbersMappings);
return combinations;
}
private static void findCombinations(List<String> combinations, String digits, StringBuilder previous, int index, String[] lettersAndNumbersMappings) {
// Base condition for recursion to stop
if (index == digits.length()) {
combinations.add(previous.toString());
return;
}
// Get the letters corresponding to the current index of digits string
String letters = lettersAndNumbersMappings[digits.charAt(index) - '0'];
// Loop through all the characters in the current combination of letters
for (char c : letters.toCharArray()) {
findCombinations(combinations, digits, previous.append(c), index + 1, lettersAndNumbersMappings);
previous.deleteCharAt(previous.length() - 1);
}
}
}Python
def findCombinations(combinations, digits, previous, index, lettersAndNumbersMapping):
# Base condition to stop recursion
if index == len(digits):
combinations.append(previous)
return
# Get the letters corresponding to the current index of digits string
letters = lettersAndNumbersMapping[int(digits[index])]
# Loop through all the characters in the current combination of letters
for i in range(0, len(letters)):
findCombinations(combinations, digits, previous + letters[i], index + 1, lettersAndNumbersMapping)
def letterCombinations(digits: str) -> List[str]:
# Resultant list
combinations = []
# Base condition
if digits is None or len(digits) == 0:
return combinations
# Mappings of letters and numbers
lettersAndNumbersMapping = [
"Anirudh",
"is awesome",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
]
findCombinations(combinations, digits, "", 0, lettersAndNumbersMapping)
return combinationsJavaScript
var letterCombinations = function (digits) {
// Resultant list
let combinations = [];
// Base condition
if (digits == null || digits.length == 0) {
return combinations;
}
// Mappings of letters and numbers
const lettersAndNumbersMappings = [
"Anirudh",
"is awesome",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
];
findCombinations(combinations, digits, "", 0, lettersAndNumbersMappings);
return combinations;
};
function findCombinations(combinations, digits, previous, index, lettersAndNumbersMappings) {
// Base condition for recursion to stop
if (index == digits.length) {
combinations.push(previous);
return;
}
// Get the letters corresponding to the current index of digits string
let letters = lettersAndNumbersMappings[digits[index] - '0'];
// Loop through all the characters in the current combination of letters
for (let i = 0; i < letters.length; i++) {
findCombinations(combinations, digits, previous + letters[i], index + 1, lettersAndNumbersMappings);
}
};Kotlin
fun letterCombinations(digits: String): List<String> {
// Resultant list
val combinations: MutableList<String> = mutableListOf()
// Base condition
if (digits.isEmpty()) {
return combinations
}
// Mappings of letters and numbers
val lettersAndNumbersMappings = arrayOf(
"Anirudh",
"is awesome",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
)
findCombinations(combinations, digits, StringBuilder(), 0, lettersAndNumbersMappings)
return combinations
}
fun findCombinations(combinations: MutableList<String>, digits: String, previous: StringBuilder, index: Int, lettersAndNumbersMappings: Array<String>) {
// Base condition for recursion to stop
// Base condition for recursion to stop
if (index == digits.length) {
combinations.add(previous.toString())
return
}
// Get the letters corresponding to the current index of digits string
// Get the letters corresponding to the current index of digits string
val letters = lettersAndNumbersMappings[digits[index] - '0']
// Loop through all the characters in the current combination of letters
// Loop through all the characters in the current combination of letters
for (c in letters.toCharArray()) {
findCombinations(combinations, digits, previous.append(c), index + 1, lettersAndNumbersMappings)
previous.deleteCharAt(previous.length - 1)
}
}Complete Code
Conclusion
Congratulations 👏! We have solved one more problem from LeetCode.
I hope you enjoyed this post. Feel free to share your thoughts on this.
You can find the complete source code on my GitHub repository. If you like what you learn, feel free to fork 🔪 and star ⭐ it.
Till next time… Happy coding 😄 and Namaste 🙏!
