HomeAboutBlogs

LeetCode #19 - Remove Nth Node From End Of List

November 15, 2020

Hello LeetCode enthusiasts 👋! It’s time to look the nineteenth problem from LeetCode.

Problem Statement

Given the head of a linked list, remove the nth node from the end of the list and return its head.

Follow up: Could you do this in one pass?

Constraints:

The number of nodes in the list is sz.

  • 1 ≤ sz ≤ 30
  • 0 ≤ Node.val ≤ 100
  • 1 ≤ n ≤ sz

Examples

Example 1: 

Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]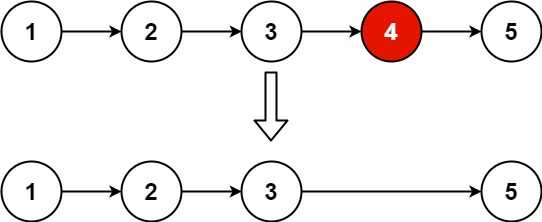
LeetCode 19 List 1 (courtesy: LeetCode)

Example 2:

Input: head = [1], n = 1
Output: []

Example 3:

Input: head = [1,2], n = 1
Output: [1]

Analysis

We are given a linked list and a number n, and we are required to remove the nth from the end of the list. Since we are removing the nth node, we need to link next pointer of (n - 1)th node to the (n + 1)th node.

Once we remove the node, we need to return the head of the modified list.

Approach

The intuitive approach can be like that — move to the end of the list and then count n nodes backwards. This works but since the given linked list is a singly linked list (where previous pointer is not present), therefore, we need to maintain the previous pointer in every step.

Also, this approach requires two traversals of the linked list, which is an overkill.

So, do we have another way to solve this? Of course, we have 😄 using Two Pointer Technique.

Two Pointer Technique

This technique is used to solve multiple linked list problems. In this, we use two pointers, slow and fast. The fast pointer sometimes —

  • Move faster than the slow pointer (two steps at a time, for example)
  • Move ahead of the slow pointer with same speed (n steps ahead, for example)

This problem also requires usage of two pointer technique where both pointers move with same speed but fast pointer is n steps ahead of slow pointer.

Imagine there are two bikers both riding Lightning LS-218 at top speed (which is 351 km/h 😲) but from different points A and B 100 km apart (B = 100 + A). Assuming they are riding with same speed then when the biker who started from A travelled 200 km, the biker would also have travelled 200 km but would be at 300 km mark (100 + 200).

We can assume biker at A as slow pointer and biker at B as fast pointer (not that A’s speed is slow but it is behind 100 km).

Applying the same logic here, we can follow below steps —

  1. Initialize two pointers slow and fast, pointing to the head of the linked list.
  2. Move fast pointer n steps ahead.
  3. Now, move both slow and fast one step at a time unless fast reaches to the end. The fast pointer will definitely reach to the end before slow because it is ahead.
  4. When we fast pointer reaches to the end, the slow pointer will be n steps behind it i.e., n steps behind the end of the list.
  5. At that point, we will remove the node and link it to the next of current node.

Thus, we only have to traverse the list only once which is more efficient.

Time Complexity

We are traversing the list only once, hence the time complexity is O(n), where n is the number of nodes in the list.

Space Complexity

We are not using any data structure for intermediate calculation, hence the space complexity will be O(1).

Code

Java

public class RemoveNthNodeFromEndOfList {

    public ListNode removeNthFromEnd(ListNode head, int n) {
        // Two pointers - fast and slow
        ListNode slow = head;
        ListNode fast = head;
        // Move fast pointer n steps ahead
        for (int i = 0; i < n; i++) {
            if (fast.next == null) {
                // If n is equal to the number of nodes, delete the head node
                if (i == n - 1) {
                    head = head.next;
                }
                return head;
            }
            fast = fast.next;
        }
        // Loop until we reach to the end.
        // Now we will move both fast and slow pointers
        while (fast.next != null) {
            slow = slow.next;
            fast = fast.next;
        }
        // Delink the nth node from last
        if (slow.next != null) {
            slow.next = slow.next.next;
        }
        return head;
    }

    static class ListNode {
        int val;
        ListNode next;

        ListNode(int val) {
            this.val = val;
        }
    }
}

Python

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next


def removeNthFromEnd(head: ListNode, n: int) -> ListNode:
    # Two pointers - fast and slow
    slow = head
    fast = head
    # Move fast pointer n steps ahead
    for i in range(0, n):
        if fast.next is None:
            # If n is equal to the number of nodes, delete the head node
            if i == n - 1:
                head = head.next
            return head
        fast = fast.next
    # Loop until fast node reaches to the end
    # Now we will move both slow and fast pointers
    while fast.next is not None:
        slow = slow.next
        fast = fast.next
    # Delink the nth node from last
    if slow.next is not None:
        slow.next = slow.next.next
    return head

JavaScript

var removeNthFromEnd = function (head, n) {
    // Two pointers - fast and slow
    let slow = head;
    let fast = head;
    // Move fast pointer n steps ahead
    for (let i = 0; i < n; i++) {
        if (fast.next === null) {
            // If n is equal to the number of nodes, delete the head node
            if (i === n - 1) {
                head = head.next;
            }
            return head;
        }
        fast = fast.next;
    }
    // Loop until we reach to the end.
    // Now we will move both fast and slow pointers
    while (fast.next !== null) {
        slow = slow.next;
        fast = fast.next;
    }
    // Delink the nth node from last
    if (slow.next !== null) {
        slow.next = slow.next.next;
    }
    return head;
};

function ListNode(val, next) {
    this.val = (val === undefined ? 0 : val)
    this.next = (next === undefined ? null : next)
}

Kotlin

fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
    // Two pointers - fast and slow
    var newHead: ListNode? = head
    var slow = newHead
    var fast = newHead
    // Move fast pointer n steps ahead
    for (i in 0 until n) {
        if (fast?.next == null) {
            // If n is equal to the number of nodes, delete the head node
            if (i == n - 1) {
                newHead = newHead!!.next
            }
            return newHead
        }
        fast = fast.next
    }
    // Loop until we reach to the end.
    // Now we will move both fast and slow pointers
    while (fast?.next != null) {
        slow = slow!!.next
        fast = fast.next
    }
    // Delink the nth node from last
    if (slow?.next != null) {
        slow.next = slow.next!!.next
    }
    return newHead
}
internal class ListNode(val `val`: Int) {
    var next: ListNode? = null
}

Complete Code

Conclusion

Congratulations 👏! We have solved the problem using two pointer technique which is very handy in solving a variety of linked list problems.

I hope you enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn, feel free to fork 🔪 and star ⭐ it.

Till next time… Happy coding 😄 and Namaste 🙏!

Created and maintained by@Anirudh Sharma
I love to learn and share. Hence, this site has no ads, no affiliation links, or any BS. If you like what you see, give me a thumbs up.

GitHub iconMedium iconTwitter iconFacebook iconLinkedIn iconStackoverflow icon